こんにちは燦です。
今回は、「統計」やります!
一次試験のなぜか経営情報システムに乱入してくるやつね。
なんで統計がここにしれっと入ってくるんじゃ?
ITと統計はなんか相性いいですからね。ほらPythonとか…。
なんかプログラミングとか全部含めて「IT」で済ますのやめてもらえます?
ほんとそのへんの定義がよくわかってません。
ただ統計学は少し勉強していますのでその目線で今回はお伝えしたいと思います。
過去14年の問題傾向
まず経営情報システムから出題される「統計問題」の履歴を見てみます。

こんな感じで毎年2問くらい出題されます。
しかも決まってほぼ最後らへんに出題されますよね。
最近は2問でないこともあるのかね?
はい、最近ちょっと傾向が変わっているように思います。
表を少し簡素化しましたのでこっちを見てください。

おや?
ずっと出てた検定の問題が急にでなくなって、分析や基礎の問題がでるようになったのか?
そうなんですよね。
なんか最近は診断協会の統計問題に対して「どう扱ったらええねん…」っていう空気をなんとなく感じます。
統計の問題は変な問題ばかり
統計をかじった身としての全体の感想なんですけど、基本的には簡単です。
そうなの?
はい、もし統計検定で出てきたら絶対に当てないといけないようなレベルのものも多いです。
診断士試験でいう「中小企業の定義」問題みたいな。
じゃあちょっと勉強したら確実に取れる?
たぶん厳しいです…。
なんでやねん!
例えるならこんな感じ?
なんかいびつな問題じゃね。
あくまでイメージですけどね…。
①さえわかれば他を考えるまでもなく超簡単に正解。
②は用語の意味さえ知っていれば簡単。もちろん算数は体育とは別物。
③は非常にマニアックで普通知らない(わからないではなくて知らない)オイラーは三角関数と複素指数函数の間に成り立つので✕。
④中途半端な知識を持ってる人へのキラー選択肢。平方根は不要。
うーん。学習し甲斐がないなぁ。
統計2級学習レベルでたぶん8割方は取れると思いますが、学習時間と取れる得点があってないんですよね…。
それに深い問題の場合、99%の受験生が当てずっぽうになる試験問題とかどうなの?って思います。
かといってきちんと基礎から理解するにはこれだけで+50~100時間は必要。
なので最近の統計的基礎知識や分析種別を答えさせる傾向は、診断士の試験としてはマッチしているように思います。
統計の問題は捨て問なのか?
というわけで確実に取っていくにはけっこうな脳の容量と時間を食いますし、しっかり学習したとしても変な問題に弄ばれるという可能性も高いです。
だから昔から統計は捨て問って言われているのね。
はい、でも2問(最近は1問?)ありますからね。
出題される可能性は非常に高いわけですからなんとか少ない勉強で得点源にしたい!というのがみんなの声ではないでしょうか。
ならポイントだけ教えてくれ!ポイントだけ。
ピンポイントで用語だけ押さえておく!
さらっと基礎用語や統計知識を身に着けておくだけで選択肢をかなり絞り込めると思います。
基礎の基礎用語
こんな問題出たら超ラッキー!
①平均値(μ=mean) データの平均
1, 3, 6, 8, 9, 9 の平均値は6
②中央値(median) データの真ん中にくるやつ
2, 4, 5, 7, 7, の中央値は5
1, 3, 6, 8, 9, 9 の中央値は7
※真ん中に2つある場合はその平均値
③平均偏差(絶対偏差) 平均との差の平均
3, 6, 6, 6, 8, 9, 9, 9(平均7)
ぞれぞれ平均7との差(絶対値)は
4, 1, 1, 1, 1, 2, 2, 2(合計14)
合計÷個数(14/8≒1.75)
※データのバラつき度合いを示す
④分散(σ^2) 平均との差の2乗の平均
3, 6, 6, 6, 8, 9, 9, 9(平均7)
ぞれぞれ平均7との差の二乗は
4, 1, 1, 1, 1, 2, 2, 2(差)
16,1, 1, 1, 1, 4, 4, 4 (差の二乗)
合計÷個数(32/8≒4)
※データのバラつき度合いを示す
⑤標準偏差(σまたはSD) 分散の√
√4=2
※データのバラつきを示す
⑥相関係数(ρ)もしくは(r)
AとBの2者の関係性を示す。
必ず-1~+1の間の値を取る。
-1: 完全に真逆の関係
+1: 完全に正の比例関係
0 : 全くの無関係
0.75: 結構相関の強い関係
↓散布図と相関係数のイメージ
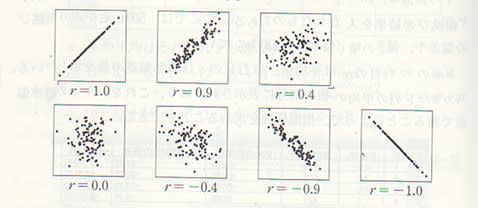
相関係数=AB共分散 / (A標準偏差σ×B標準偏差σ)
※覚え方:単純に分散/分散として比較しているだけの話(分散=σ×σ)
もしAとAの相関係数を求めるならA分散/A分散なので当然相関係数は1
自分と自分の関連性は100%といってる意味と同じ。
AとBの関連性を求める場合に、少しひねってAB共分散/Aσ×Bσとなる。
+αの知識でライバルと差をつけろ!
①変動係数 (標準偏差/平均値)
標準偏差が10と20だったらどちらのデータがバラついている??
20といいたいところですが、元データが分からないと比較できません。
A) 100点満点で平均点50点のテストで標準偏差10
B) 1000点満点で平均点500点のテストで標準偏差20
だとどうでしょうか。直感的にAのバラついてそう…とわかりますか?
100円のジュースが110円になると「むむっ」と思いますが、258,000円の洗濯機が258,020円になっていても別になんとも思わないですよね。
つまり平均値の数値で割って比較すればいいです。
A)10/50=0.2
B)20/500=0.04
つまり変動係数はAの方が大きいのでAの方がバラついているとなります。
②SD度 (平均値との差/標準偏差)
標準偏差SDで、その度合いを測ります。
平均70点(標準偏差8)のテストを受けていたとします。
自分が78点でした。その場合SD度は1です。(+1SD)
もし86点だったらSD度は2です。(+2SD)
62点だったらSD度は-1です。(-1SD)
お分かりの通り平均との差を標準偏差で割ったものがSD度です。
93点だったなら、(93-70)/8=2.875(+2.875SD)ですね。
③偏差値 (10SD+50)
上で出したSD度から簡単に導き出せます。
SD度×10+50です。SD度の時点でどれくらいすごいかはすぐわかるわけですが、SD度がマイナスというのはなんか人間として劣っているような印象を与えますので、×10して+50してあげてるみたいです。
平均70点(標準偏差8)のテストでもし90点を取ったなら、SD度は+2.5SD
つまり2.5×10+50=75 偏差値は75となります。
④標準誤差(SE) (標準偏差σ/√平均データ数)
標準偏差よりもう少し大きな概念で平均値のバラつきを示します。
これを一から理解するのは手間なので、標準偏差をデータ数√したもので割るという認識でいいと思います。
標準誤差は検定で死ぬほど使います。診断士試験でもたまに出てきていますね。
SE=σ/√n(n=データ数) あるいは=√(分散/n)でも同じ意味
⑤ヒストグラム
総計の全てのベースともいえるグラフ
位毎にデータ数を数えたもの
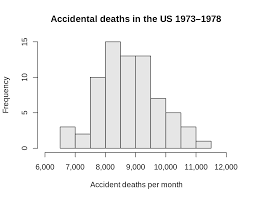
⑥正規分布
ヒストグラムを左右対称で理想形にしたもの
確率の分布なので△の面積の合計は1
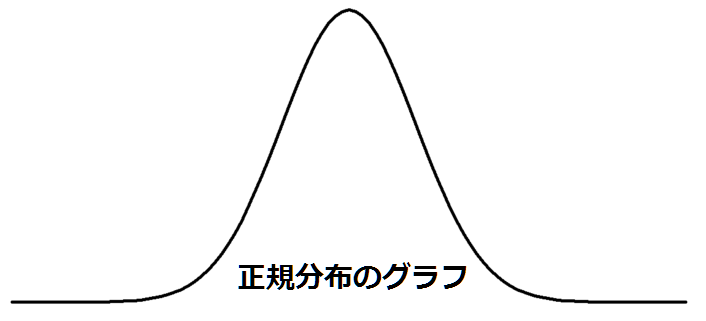
⑦標準正規分布
正規分布を標準化したもの。全ての原点になる分布図です。
初期アバターみたいなものでしょうか。
下の-5~+5のメモリは先ほどのSD度のことになります。
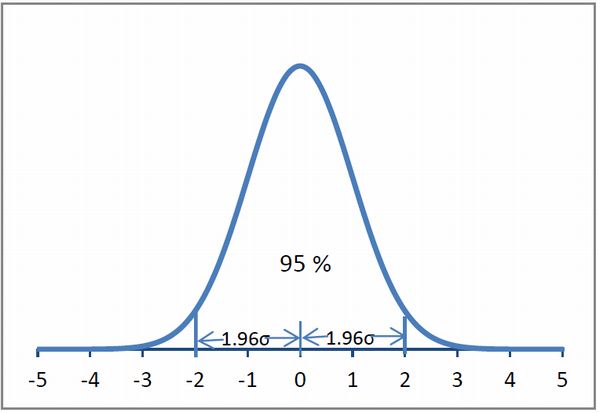
SD度1.96(=1.96σ)という位置に注目してほしいのですが、この位置で全体の95%を占めます。
この95%という数字は統計において非常に重要です。
よくみますよね?有意水準95%で~とか。
そもそも世の中で100%断定出来る事ってありませんよね?
明日も生きてる確率も絶対に100%とは言えないわけです。
だから統計の世界では、95%以上ならとりあえずそれでよくね?
ってやるわけです。(99%でやる場合もある)
それが有意水準95%で判断する(検定)ということであり、その時に出てくる標準正規分布の1.96という数字は特別な意味を持ちます。
ちなみに偏差値の話でいうと偏差値70の人は+2SDなわけですから、1.96の点よりも右側に位置するということになりますね。
つまり上位2.5%以内に属するということなります。
1000人いれば上から20位くらい?すごいですね。
また診断士試験は上位20%以上で基本合格ですから、SD度でいうと+0.84くらいの位置です。
つまり偏差値58.4以上で合格です。だから何って話ですが…。
その2へ続く